On A 32 Bit Processor, How Many Bits Are Contained In Each Floating-point Data Registers?

Fixed Point and Floating Signal Number Representations

Digital Computers apply Binary number system to represent all types of data inside the computers. Alphanumeric characters are represented using binary bits (i.e., 0 and ane). Digital representations are easier to design, storage is like shooting fish in a barrel, accuracy and precision are greater.

In that location are various types of number representation techniques for digital number representation, for case: Binary number system, octal number arrangement, decimal number arrangement, and hexadecimal number arrangement etc. But Binary number system is about relevant and pop for representing numbers in digital reckoner arrangement.

Storing Real Number

These are structures as following beneath −

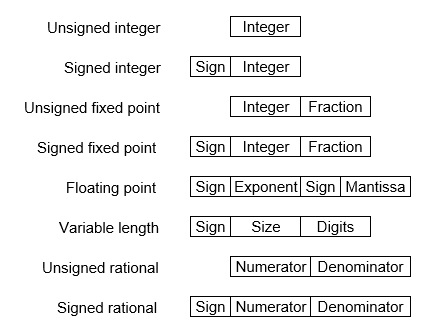
There are two major approaches to store real numbers (i.e., numbers with fractional component) in modern computing. These are (i) Fixed Point Notation and (two) Floating Point Notation. In fixed point note, at that place are a stock-still number of digits after the decimal point, whereas floating betoken number allows for a varying number of digits afterwards the decimal indicate.

Stock-still-Point Representation −

This representation has fixed number of bits for integer function and for fractional part. For example, if given stock-still-betoken representation is IIII.FFFF, and then you tin store minimum value is 0000.0001 and maximum value is 9999.9999. At that place are three parts of a stock-still-indicate number representation: the sign field, integer field, and fractional field.

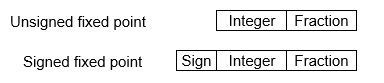
We can represent these numbers using:

Signed representation: range from -(2^(grand-1)-1) to (2^(k-ane)-i), for yard $.25.
1'southward complement representation: range from -(2^{(one thousand-ane)}-1) to (2^(k-1)-ane), for 1000 bits.
2's complementation representation: range from -(two^(k-one)) to (2^(k-one)-one), for k bits.

2'south complementation representation is preferred in computer organisation because of unambiguous holding and easier for arithmetics operations.

Example −Presume number is using 32-fleck format which reserve 1 chip for the sign, 15 bits for the integer part and sixteen $.25 for the fractional part.

So, -43.625 is represented as post-obit:

Where, 0 is used to represent + and 1 is used to represent. 000000000101011 is 15 scrap binary value for decimal 43 and 1010000000000000 is 16 flake binary value for partial 0.625.

The advantage of using a fixed-point representation is performance and disadvantage is relatively express range of values that they can represent. So, information technology is usually inadequate for numerical analysis equally it does not permit enough numbers and accuracy. A number whose representation exceeds 32 bits would take to be stored inexactly.

These are higher up smallest positive number and largest positive number which tin be store in 32-bit representation as given higher up format. Therefore, the smallest positive number is two^-16 ≈ 0.000015 guess and the largest positive number is (2^xv-1)+(1-2^-16)=ii^xv(1-2^-16) =32768, and gap between these numbers is 2^-xvi.

We can movement the radix point either left or correct with the help of only integer field is 1.

Floating-Point Representation −

This representation does not reserve a specific number of $.25 for the integer part or the fractional role. Instead it reserves a certain number of $.25 for the number (chosen the mantissa or significand) and a certain number of bits to say where within that number the decimal place sits (called the exponent).

The floating number representation of a number has two part: the beginning office represents a signed fixed point number chosen mantissa. The second role of designates the position of the decimal (or binary) point and is chosen the exponent. The stock-still betoken mantissa may be fraction or an integer. Floating -point is always interpreted to represent a number in the following class: Mxr^e.

Only the mantissa chiliad and the exponent e are physically represented in the annals (including their sign). A floating-point binary number is represented in a like mode except that is uses base two for the exponent. A floating-point number is said to be normalized if the most significant digit of the mantissa is 1.

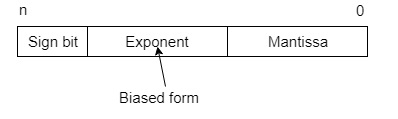
And so, actual number is (-1)^south(ane+m)x2^{(due east-Bias)}, where sis the sign bit, one thousandis the mantissa, eis the exponent value, and Biasis the bias number.

Note that signed integers and exponent are represented past either sign representation, or one'south complement representation, or two's complement representation.

The floating point representation is more flexible. Any non-zero number can be represented in the normalized form of ±(1.b₁b₂b_iii ...)₂x2^northward This is normalized form of a number x.

Case −Suppose number is using 32-bit format: the one bit sign fleck, 8 bits for signed exponent, and 23 bits for the partial part. The leading bit ane is not stored (equally it is ever 1 for a normalized number) and is referred to equally a "hidden bit".

Then −53.5 is normalized as -53.v=(-110101.1)₂=(-ane.101011)x2⁵ , which is represented as following beneath,

Where 00000101 is the viii-bit binary value of exponent value +5.

Notation that viii-bit exponent ﬁeld is used to store integer exponents -126 ≤ northward ≤ 127.

The smallest normalized positive number that ﬁts into 32 bits is (1.00000000000000000000000)₂x2^-126=ii^-126≈1.18x10^-38 , and largest normalized positive number that ﬁts into 32 bits is (i.11111111111111111111111)_iix2¹²⁷=(2²⁴-1)x2¹⁰⁴ ≈ 3.40x10³⁸ . These numbers are represented as following below,

The precision of a ﬂoating-point format is the number of positions reserved for binary digits plus ane (for the hidden bit). In the examples considered hither the precision is 23+1=24.

The gap betwixt ane and the adjacent normalized ﬂoating-point number is known as machine epsilon. the gap is (i+two^-23)-one=ii^-23for to a higher place case, only this is same as the smallest positive ﬂoating-bespeak number considering of non-compatible spacing dissimilar in the ﬁxed-point scenario.

Annotation that non-terminating binary numbers can be represented in floating point representation, e.g., 1/3 = (0.010101 ...)₂ cannot exist a ﬂoating-point number as its binary representation is non-terminating.

IEEE Floating point Number Representation −

IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation as post-obit diagram.

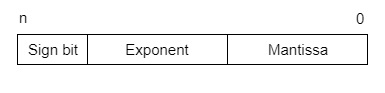
So, actual number is (-1)^s(1+m)x2^(e-Bias), where sis the sign fleck, mis the mantissa, due eastis the exponent value, and Biasis the bias number. The sign fleck is 0 for positive number and 1 for negative number. Exponents are represented past or two's complement representation.

Co-ordinate to IEEE 754 standard, the floating-point number is represented in following ways:

Half Precision (16 bit): 1 sign bit, 5 bit exponent, and ten bit mantissa
Single Precision (32 bit): ane sign bit, viii bit exponent, and 23 bit mantissa
Double Precision (64 bit): 1 sign bit, eleven bit exponent, and 52 flake mantissa
Quadruple Precision (128 scrap): ane sign bit, 15 bit exponent, and 112 bit mantissa

Special Value Representation −

There are some special values depended upon unlike values of the exponent and mantissa in the IEEE 754 standard.

All the exponent $.25 0 with all mantissa bits 0 represents 0. If sign flake is 0, then +0, else -0.
All the exponent bits one with all mantissa $.25 0 represents infinity. If sign bit is 0, then +∞, else -∞.
All the exponent bits 0 and mantissa bits non-zero represents denormalized number.
All the exponent bits 1 and mantissa bits non-zero represents fault.

Published on 21-Feb-2019 10:46:22

Related Questions & Answers
Decimal stock-still signal and floating point arithmetics in Python
Format floating point number in Java
Signed floating point numbers
C++ Floating Signal Manipulation
Stock-still Point in Python
Floating indicate operators and associativity in Java
Floating-point hexadecimal in Java
Floating point comparison in C++
PHP Floating Bespeak Data Type
Convert a floating point number to string in C
What are C++ Floating-Bespeak Constants?
Floating-point conversion characters in Java
Format floating point with Java MessageFormat
How to deal with floating indicate number precision in JavaScript?
Floating Point Operations and Associativity in C, C++ and Java